感应电机启动计算说明

在感应电机选型及校核过程中，为了判断电机启动能否成功，以及不同启动方式下的启动时间和启动过程中的I-t的变化曲线，需要对启动过程进行计算。

电机与负载对，即电力拖动系统能够成功启动的关键在于转矩，即在整个启动过程中，电机产生的转矩一直大于负载本身的转矩，直到启动结束，电机和负载的转矩达到平衡。

       设电机产生的转矩为T，以电机转矩的方向为正方向，则负载转矩为-T_L，电机旋转驱动系统转矩的平衡方程式为

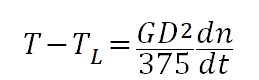
公式1

其中T-T_L为转矩差值，T-T_L>0时，启动加速；T-T_L=0时，速度平衡；T-T_L<0时，启动减速。对于负载来说，忽略负载变化的影响，不同的转速可能对应不同的负载转矩，即负载启动转矩为速度的函数： 。而对于电机来说，除了速度之外，不同的启动方式，不同的电源电压，都会影响电机的启动转矩。 为拖动系统总的飞轮力矩，由设备的机械特性决定，为固定值。为电机的转速，单位为。为启动时间，单位为秒。dn/dt即为启动过程中的速度变化率。所以启动计算的关键，在于求出在不同的启动时间，T以及T_L的值。

在下面的讨论中，我们以直连驱动，三相异步感应电机为例，介绍启动计算的过程。

电机供应商会提供电机的T-n曲线，I-n曲线，以及电机的转动惯量等数据。设备制造厂家也需要提供负载设备的T-n曲线，转动惯量等数据。在计算中，由于dn/dt的微分算式存在，为便于计算机进行数字化计算，采用微小时间片划分方式，将dn/dt转换为，将公式1转换为

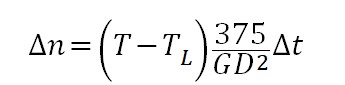
公式2

其中微小时间片=0.01秒，则每一步可以计算出0.01秒时间内的速度增量，将速度增量加到当前速度上，则为下一个时间片的速度。

初始化启动时间和启动速度均为0。通过供应商提供的T-n，I-n曲线等，可以得出在n=0的初始速度下的，，等，进而求出在第一个时间0.01秒内的速度增量。有了速度的增量，则可以根据当前速度（第一个迭代周期为0）和速度增量进行下一个的计算迭代。将速度增量加上当前速度，作为下一次迭代的速度值，根据供应商的T-n曲线，求出在下一次迭代的速度值时相应的T，再根据公式2，求出此次迭代的速度增量。在计算机计算中，可以非常方便的进行重复迭代的运算求解，直至启动完成，从而算出相应的启动时间，I-t曲线等。

不同电压对启动时间的影响：

根据电力拖动公式，电机的启动转矩和电压的平方成正比。而启动时间又依赖电机启动转矩的大小，因此，启动电压的变化对启动时间有显著的影响。

启动成功及启动完成的判断：

启动成功与否，包含两个方面的考量：启动速度与启动电流。电机启动成功后，电流应该从启动过程中很大的启动电流（一般为3~7倍In）降到足够低（接近In）,同时速度应该上升到接近额定转速（一般在同步转速*（1-转差率）附近）。从电机的启动转矩上看，启动电流速度的增加，肯定会带来启动电流的降低，所以两个指标是等效的。当在最大启动时间内，两个指标均完成后，则认为电机的启动完成了。